Data Structures & Algorithms - Linked List: Detect Cycle

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

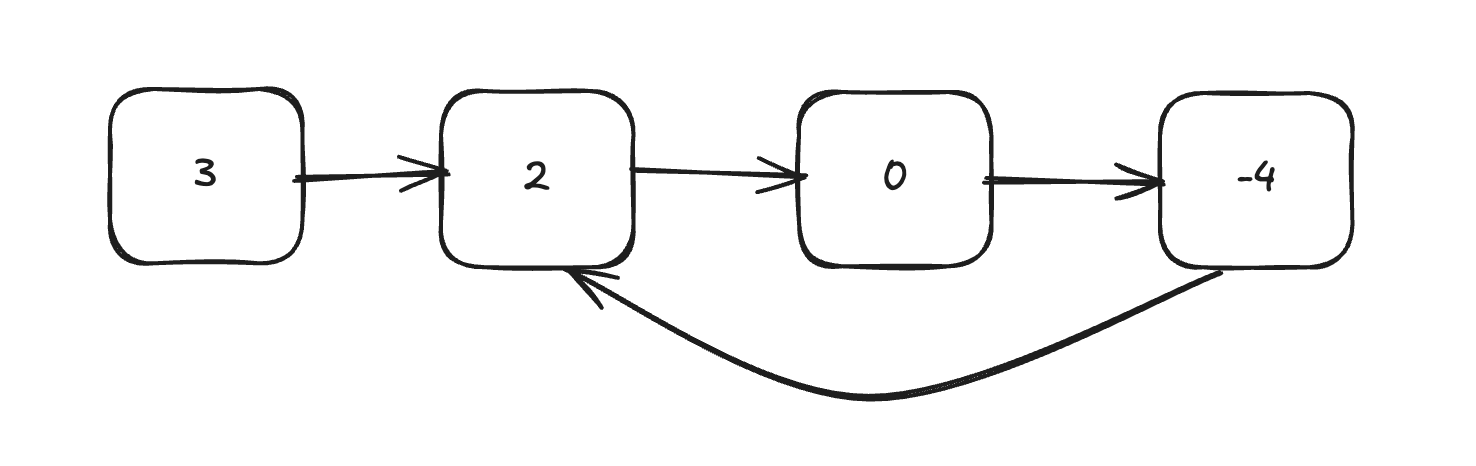
Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: true

Playground: Leetcode 141

Approach 1: Visited Set

Iterate through the linked list and use a hash set to keep track of the visited nodes. During each iteration, check if the node is already in the set. If yes, that node is the start of the cycle, otherwise add it and continue.

Algorithm

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */

- hashSet = new HashSet();
- ListNode curr = head;

- while curr != null:
    - if curr in hashSet:
        - return true;
    - hashSet.add(curr);
    - curr = curr.next;

- return false;

Visualization

Time Complexity

We may iterate over the linked list once. Hence, overall time complexity = O(n).

Space Complexity

The hash set will store at most n elements. Hence, overall space complexity = O(n).

Approach 2: Floyd Cycle Detection

A cycle in a linked list can be thought of as an infinite strip.

Assume you have two pointers on an infinite strip separated by a distance of k units. If you starting moving the first pointer (behind) by 2 units and the second pointer (ahead) by 1 unit, the distance between the two pointers will start decreasing by 1 unit in each iteration and will eventually reduce to 0, i.e., the two pointers will collide.

Algorithm

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */

- slow = head;
- fast = head;

// fast = null -> we are already at the end of the list
// fast.next = null -> we are at the last node, the list ends here
- while fast != null and fast.next != null: 
    - slow = slow.next;
    - fast = fast.next.next;

    - if slow == fast: return true; // cycle detected

- return false;

Visualization

Time Complexity

Even though we use two pointers, we do not traverse the list multiple times. Let’s break it into two possible use cases.

1 → 2 → 3 → 4 → 5 → null

The fast reaches the end in at most n/2 iterations. Considering, each iteration is O(1), the overall time complexity = O(n).

Assume:

• k = number of nodes before the cycle starts
• c = number of nodes inside the cycle

The traversal can be split into two linear phases.

In the first phase, both pointers move through the non-cyclic part of the linked list. The slow pointer advances one step at a time and reaches the start of the cycle in k steps, while the fast pointer (moving twice as fast) also enters the cycle within at most k steps. Therefore, this phase takes O(k) time.

Once both pointers are inside the cycle, the fast pointer moves one node closer to the slow pointer in every iteration, so the gap between them keeps shrinking. Because the cycle has c nodes, they are guaranteed to meet within at most c iterations, making this phase run in O(c) time.

Hence, overall time complexity = O(k + c) = O(n).

Space Complexity

We are not using any extra space. Hence, overall space complexity = O(1).